Matrix polynomial
Not to be confused with Polynomial matrix.
In mathematics, a matrix polynomial is a polynomial with matrices as variables. Examples include:
-
- where P is a polynomial,
- and I is the identity matrix.
- the commutator of A and B.
A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. If  , (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation
, (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation  .
.
A matrix polynomial identity is a matrix polynomial equation which holds for all matricies A in a specified matrix ring Mn(R).
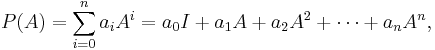
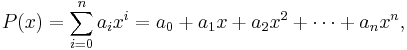
![\left[A,B\right] = A B - B A,](/2012-wikipedia_en_all_nopic_01_2012/I/287c6d535fa578a82901224aa1c187bc.png)